naoya_t@topcoder

SRM426

11.22+.2008

TopCoder参加11回目。necocenさんと同じ部屋。

DIV	level	問題名	競技中	後で	System Test	備考
1	250	ShufflingMachine	◎			95.20%
1	500	CatchTheMice	途中	o	passed	11/23 https://topcoder-g-hatena-ne-jp.jag-icpc.org/n4_t/20081123/p2
1	1000	(LongStraightRoad)	-

250点問題: ShufflingMachine

→OK。121.75点

題意を汲み取るのに時間がかかってしまった。

500点問題: CatchTheMice

→時間切れ

いい線まで行ってたけど時間が足りず。

• x軸y軸別々に交点を求め、調べるべき時刻を得るところまでは行けた。
• その時刻の間にx軸最大とy軸最大が入れ替わる点があるのでそれを求める必要があった
• エリアは無限大なので±2000を超えるエリアでクロスすることもある
• 続きはこの下

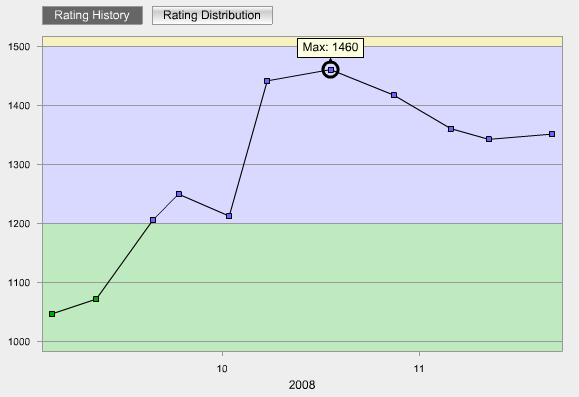
レーティングは下げ止まり、微かに上昇：1342 → 1351

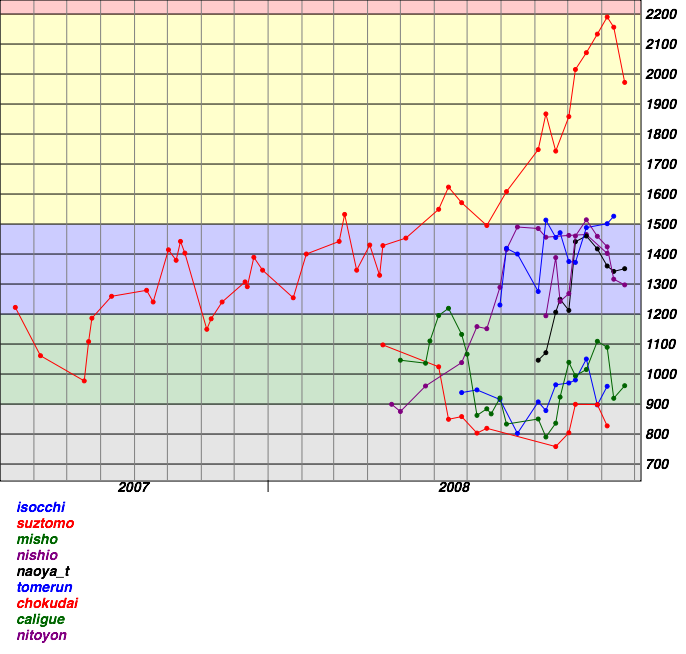
以前にisocchiさんが作ってくれたTopCoder部のレーティング比較グラフのようなものを作ってくれるところを見つけたので貼ってみる

SRM426 Div1 Medium: CatchTheMice

過去問, 練習 | 18:11 |

解けなかった500点問題に挑戦

ある時刻 t(≧0) における鼠#iの座標が ( xp[i] + xv[i]*t, yp[i] + yv[i]*t ) で与えられている。

で、全鼠を収める正方形（の籠）が最小になる時の辺の長さを求める。

上のほうの人は二分探索とか三分探索とかしてるようですが...

• ある時刻における全鼠のx座標のmaxとminの差、そしてy座標のmaxとminの差が得られるとしたら、その大きい方が籠の大きさで、
• どの鼠がx (y)各軸上でmax（あるいはmin）の位置に来るか、が切り替わるのは軌跡のx成分（y成分）が入れ替わる時刻。（座標は１次式だし、これは50匹なのですぐに全部求められる）
• x軸またはy軸で入れ替えが起こる時刻をすべて（高々1225個程度）求めたら、各時刻 t_i における全鼠の位置座標を求め、xy各軸上のmax,minを得る。
• x座標のmaxとminの差、y座標のmaxとminの差が得られる。この大きい方が時刻 t_i における籠の最小サイズ。
• ある入れ替わり時刻 t_i ではx座標の差が大きく、隣接する入れ替わり時刻 t_i±1 ではy座標の差が大きい場合（vice versa）、大きくなる座標が入れ替わる。この入れ替わる時刻も簡単な１次式で求められるので、その時刻における籠の最小サイズも求める。＜競技中にはここまで気がつかなくて数が合わなかった＞
• 以上で求めた籠の最小サイズで最も小さいものの辺の長さが答え。
• エリアの広さは無限大なので、鼠の初期位置である±1000を超えるエリアでクロスすることもある点にチュウ意。

#include <string>
#include <vector>
#include <set>
#include <list>
#include <queue>
#include <algorithm>
#include <sstream>
#include <cmath>
#include <float.h> // DBL_MAX
using namespace std;

#define sz(a)   int((a).size())
#define pb      push_back
#define all(c)  (c).begin(),(c).end()
#define tr(c,i) for(typeof((c).begin()) i=(c).begin(); i!=(c).end(); i++)

double maxnum = DBL_MAX; // 平面が無限遠に伸びているので2000とか10000とかでは駄目です

class CatchTheMice {
public:
  double largestCage(vector<int> xp, vector<int> yp, vector<int> xv, vector<int> yv) {
    int n=xp.size(); // 1..50

    set<double> tx;
    tx.clear();

    // 全鼠総当たりで（高々1225通り）
    for (int i=0;i<n;i++) {
      for (int j=0;j<n;j++) {
        if (i < j)  {
          // x座標上で追い越し／追い越される時刻を得て
          if (xv[i] != xv[j]) {
            double t = (double)(xp[i] - xp[j]) / (double)(xv[j] - xv[i]);
            if (t > 0.0) tx.insert(t); // >0ならsetに放り込む。
          }
          // y座標上で追い越し／追い越される時刻を得て
          if (yv[i] != yv[j]) {
            double t = (double)(yp[i] - yp[j]) / (double)(yv[j] - yv[i]);
            if (t > 0.0) tx.insert(t); // 同様。重複はsetが良きに計らってくれる
          }
        }
      }
    }

    // t=0 における全鼠の座標と、wx=(x最大-x最小), wy=(y最大-y最小) を求めておく
    double wx_, wy_, t_ = 0.0; // ここでアンダーバーは「１つ前の値」マーク
    {
      double xmin = maxnum, xmax = -maxnum, ymin = maxnum, ymax = -maxnum;
      for (int i=0;i<n;i++) {
        double x = (double)xp[i];
        double y = (double)yp[i];
        if (x < xmin) xmin = x;
        if (x > xmax) xmax = x;
        if (y < ymin) ymin = y;
        if (y > ymax) ymax = y;
      }
      wx_ = xmax - xmin;
      wy_ = ymax - ymin;
    }
    double mmw = max(wx_,wy_); // 籠の大きさ

    // setに放り込んでおいた時刻をイテレータで順に取り出して
    // それぞれの時刻における全鼠の座標を算出し、
    // wx=(x最大-x最小), wy=(y最大-y最小) を求める。
    tr(tx,it) {
      double t = *it;
      double xmin = maxnum, xmax = -maxnum, ymin = maxnum, ymax = -maxnum;
      for (int i=0;i<n;i++) {
        double x = t*xv[i] + xp[i];
        double y = t*yv[i] + yp[i];
        if (x < xmin) xmin = x;
        if (x > xmax) xmax = x;
        if (y < ymin) ymin = y;
        if (y > ymax) ymax = y;
      }
      double wx = xmax - xmin;
      double wy = ymax - ymin;

      if (((wx_ < wy_ && wx > wy) || (wx_ > wy_ && wx < wy))) {
        // wx,wyの最大をとる座標軸が入れ替わる場合
        double dx = wx - wx_, dy = wy - wy_;
        double w = (wx_ * dy - wy_ * dx) / (dy - dx); // wはこの時刻における籠の大きさの最小値
        // printf("crossing between t=%g and t=%g... at %g\n", t_, t, (wx_ - wy_) / (dy - dx) );
        if (w < mmw) mmw = w;
      } else {
        // 入れ替わらない場合
        double w = max(wx,wy);
        if (w < mmw) mmw = w;
      }
      wx_ = wx;
      wy_ = wy;
      t_ = t;
    }

    return mmw;
  }
};

日本人参加者のランキングとか

18:11 |

https://www.otinn.com/groups/view_group.php?gid=1376