2010-09-09
SRM481
総括
250: 161.83/passed system test
500: 217.42/passed system test
900: Unopened
--------------
379.25p + 0p
Room: #2/19
DivI: #90/704
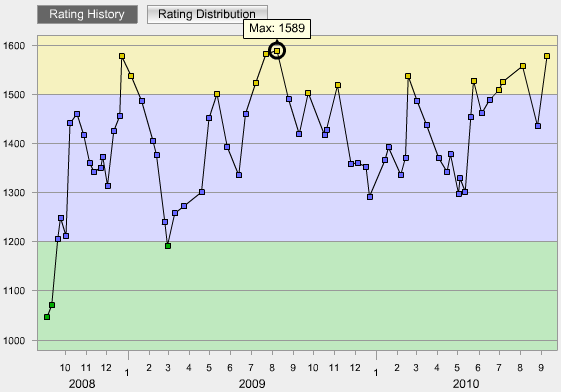
Rating: 1436→1577 前々回より上がってるからよしとしよう
脳内解説
ネタバレになる程度には書いた
Easy(250): ChickenOracle
- あーこういうの苦手
- コインの裏表とか、オセロの白黒とかバリエーションがあるよね
- しかもこの問題文わかりにくい
- で。問題文を読んだところで、サンプルケースの数字と説明を見ながら論理の検証をする。というか、どういう足し算引き算をすれば答えが合うのかパターンをあれこれ考えた(がハズレばかり)。
- ちゃんと筋道を立てて考えよう。
- 真の答えが卵だった場合と鶏だった場合がある
- オラクルから嘘を聞いた人数が固定なので、聞いた答えの分布はそれぞれのケースで固定
- 答えを聞いた人のうち何人が嘘を言うかは分かっているが、どちらの答えを聞いた人がどれだけかは分からない → でも総当たりで行けそう。
- あり得るシナリオをチェック。卵、鶏、両方に可能性があればambiguous、どちらもありえなければlie。
- これだ
- 答え合わない。ああ。場合分けのそれぞれに対し卵でない場合に鶏、みたいな余分なチェックが入ってた。
- 外した。でも答え合わない。
- 嘘つきの分布の総当たりが総当たってなかった。0〜Nまで見るべきところで0〜N-1みたいな。直した。答えが合うようになった。
- submitted. 161.83点。だいぶ出遅れた感じ。
Medium(500): BatchSystemRoulette
- まず、所要時間がそれぞれ1,2,3,4分の4つの仕事があったとして、平均待ち時間が最短になるのはどういう並べ方の時?
- 4,3,2,1と1,2,3,4を比べたら1,2,3,4の方が短かった。たぶんこういう感じだろう(※証明なし)
- 2,3の担当者が同じ人だったら?
- 担当者毎にまとめて 1,4,2+3 でよさげ(※証明なし)
- 2,3の順列は同確率で分布
- 1,1,2,2,2とかだったら?
- 所要時間が同じもの同士でグループを形成し、その中で何番目になるかは同確率で分布
- 平均待ち時間が最短になるときの、各仕事の待ち時間の期待値をこんな感じで求めたい
- とか前にもこういうタイプの問題なかった?
- さあやるか。
- 担当者毎に仕事をまとめ、合計時間を調べ、合計時間Tの短い人から見ていく。開始時刻S=0。
- 担当者ごとに、手持ちの仕事の並び順の全順列組み合わせについて検討し、待ち時間の期待値を求める…とかやってたらTLE食らうに決まってる
- 担当者Aの仕事がK個あるなら、それぞれの仕事がk番目に行われる確率は1/K…とかどうでもいいんです実は(ていうか。ひらめいちゃったもんね)
- 担当者Aの仕事の1つ(Jとしよう)について見たとき、担当者Aの他の仕事(K-1個ありますね)がJの前に来るか後に来るかは50%-50%じゃないか?とすると、Jの待ち時間に関係あるのは前に来た時だけなので、Jの待ち時間の期待値は
- (担当者Aの仕事の開始時刻の期待値) + (担当者Aの全仕事の合計時間 - 仕事Jの所要時間)/2 + (仕事Jの所要時間)
- ではあるまいか。場合分けするまでもないけど、仕事が1つの場合は
- (担当者Aの仕事の開始時刻の期待値) + (仕事Jの所要時間)
- で普通に求まる。
- コードかきかき
- 計算どんぴしゃ
- 提出…?あと5分ぐらい残ってるから落ち着いて。そういえば制約条件に1e9みたいな数字なかった?そういう時はintに危険信号。INT_MAXを超えるかもしれない変数をlong longに差し替えてからsubmit。
- 217.42点。残り時間2分ぐらい。
Hard(900): (unopened)
- 開いてない。
Challenge Phase
- 見てるだけでした
提出全コード
Easy(250): ChickenOracle
#include <string>
#include <vector>
#include <set>
#include <map>
#include <list>
#include <queue>
#include <algorithm>
#include <sstream>
#include <cmath>
using namespace std;
#define rep(var,n) for(int var=0,lim=(n);var<lim;var++)
#include <cstdio>
class ChickenOracle {
public:
string theTruth(int n, int eggCount, int lieCount, int liarCount) {
int chCount = n-eggCount;
int pe=0, pc=0;
int a=n-lieCount, b=lieCount;
rep(la,liarCount+1){
int lb=liarCount-la;
if (la>a || lb>b) continue;
int ax=a-la+lb;
if (eggCount==ax) pe=1;
}
rep(la,liarCount+1){
int lb=liarCount-la;
if (la>a || lb>b) continue;
int ax=a-la+lb;
if (chCount==ax) pc=1;
}
if (pe==1 && pc==1) return "Ambiguous";
else if (pe==1) return "The egg";
else if (pc==1) return "The chicken";
else return "The oracle is a lie";
}
};
Medium(500): BatchSystemRoulette
#include <string>
#include <vector>
#include <set>
#include <map>
#include <list>
#include <queue>
#include <algorithm>
#include <sstream>
#include <cmath>
#include <cstdio>
using namespace std;
typedef long long ll;
#define sz(a) int((a).size())
#define pb push_back
#define rep(var,n) for(int var=0,lim=(n);var<lim;var++)
#define all(c) (c).begin(),(c).end()
#define tr(c,i) for(__typeof__((c).begin()) i=(c).begin(); i!=(c).end(); i++)
#define found(s,e) ((s).find(e)!=(s).end())
class BatchSystemRoulette {
public:
vector <double> expectedFinishTimes(vector <int> duration, vector <string> user) {
int n=sz(duration);
vector<int> ids(n,-1);
int id=0;
map<string,int> mp; // uname,id
map<int,ll> psum; // id,sum
map<int,vector<int> > pn; //id,[i]
rep(i,n){
if (!found(mp,user[i])) {
int id_ = id++;
psum[id_] = duration[i];
pn[id_] = vector<int>(1,i);
ids[i] = mp[user[i]] = id_;
} else {
int id_ = ids[i] = mp[user[i]];
psum[id_] += duration[i];
pn[id_].pb(i);
}
}
map<ll,vector<int> > mo; //psum,i
rep(i,id){
ll ps=psum[i];
if (!found(mo,ps)){
mo[ps] = vector<int>(1,i);
}else{
mo[ps].pb(i);
}
}
vector<double> ans(n, 0.0);
ll hd =0;
tr(mo,it){
ll t = it->first;
int m=sz(it->second);
rep(j,m){
double w = 0.5*(m+1);
double te = hd + t*w, tb = te - t;
int i = it->second[j];
int u=sz(pn[i]);
if (u==1) {
int k=pn[i][0];
ans[k] = te;
} else {
ll sm=0;
rep(d,u){
int k=pn[i][d];
sm += duration[k];
}
rep(d,u){
int k=pn[i][d];
ans[k]=tb+duration[k]+0.5*(sm-duration[k]);
}
}
}
hd += t*m;
}
return ans;
}
};
コメント
トラックバック - https://topcoder-g-hatena-ne-jp.jag-icpc.org/n4_t/20100909