naoya_t@topcoder

SRM426

11.22+.2008

TopCoder参加11回目。necocenさんと同じ部屋。

DIV	level	問題名	競技中	後で	System Test	備考
1	250	ShufflingMachine	◎			95.20%
1	500	CatchTheMice	途中	o	passed	11/23 https://topcoder-g-hatena-ne-jp.jag-icpc.org/n4_t/20081123/p2
1	1000	(LongStraightRoad)	-

250点問題: ShufflingMachine

→OK。121.75点

題意を汲み取るのに時間がかかってしまった。

500点問題: CatchTheMice

→時間切れ

いい線まで行ってたけど時間が足りず。

• x軸y軸別々に交点を求め、調べるべき時刻を得るところまでは行けた。
• その時刻の間にx軸最大とy軸最大が入れ替わる点があるのでそれを求める必要があった
• エリアは無限大なので±2000を超えるエリアでクロスすることもある
• 続きはこの下

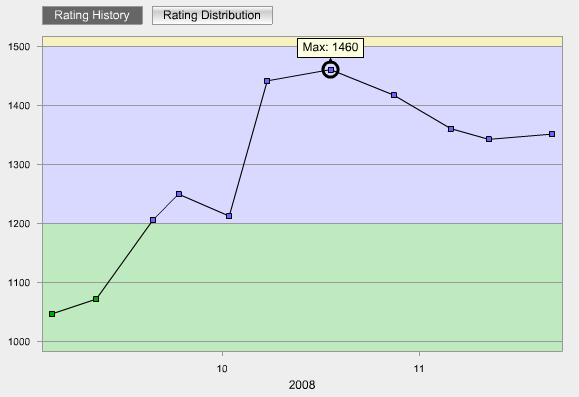
レーティングは下げ止まり、微かに上昇：1342 → 1351

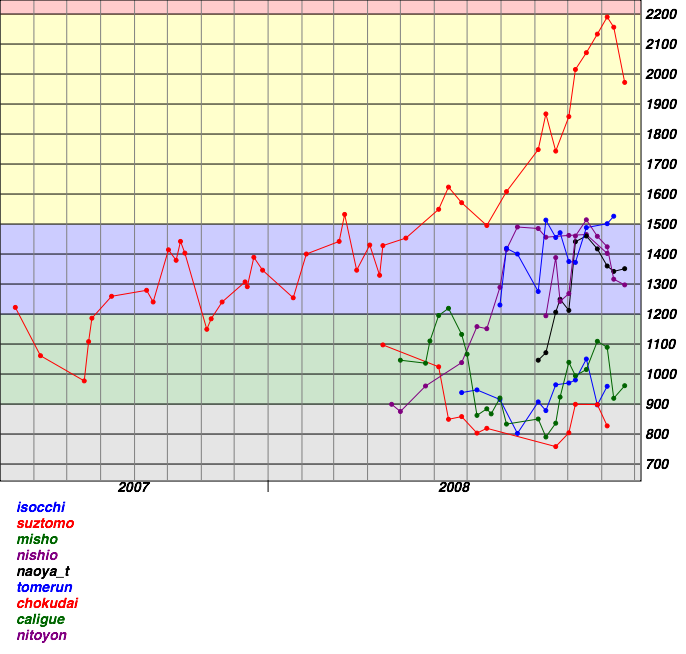
以前にisocchiさんが作ってくれたTopCoder部のレーティング比較グラフのようなものを作ってくれるところを見つけたので貼ってみる

SRM426 Div1 Medium: CatchTheMice

過去問, 練習 | 18:11 |

解けなかった500点問題に挑戦

ある時刻 t(≧0) における鼠#iの座標が ( xp[i] + xv[i]*t, yp[i] + yv[i]*t ) で与えられている。

で、全鼠を収める正方形（の籠）が最小になる時の辺の長さを求める。

上のほうの人は二分探索とか三分探索とかしてるようですが...

• ある時刻における全鼠のx座標のmaxとminの差、そしてy座標のmaxとminの差が得られるとしたら、その大きい方が籠の大きさで、
• どの鼠がx (y)各軸上でmax（あるいはmin）の位置に来るか、が切り替わるのは軌跡のx成分（y成分）が入れ替わる時刻。（座標は１次式だし、これは50匹なのですぐに全部求められる）
• x軸またはy軸で入れ替えが起こる時刻をすべて（高々1225個程度）求めたら、各時刻 t_i における全鼠の位置座標を求め、xy各軸上のmax,minを得る。
• x座標のmaxとminの差、y座標のmaxとminの差が得られる。この大きい方が時刻 t_i における籠の最小サイズ。
• ある入れ替わり時刻 t_i ではx座標の差が大きく、隣接する入れ替わり時刻 t_i±1 ではy座標の差が大きい場合（vice versa）、大きくなる座標が入れ替わる。この入れ替わる時刻も簡単な１次式で求められるので、その時刻における籠の最小サイズも求める。＜競技中にはここまで気がつかなくて数が合わなかった＞
• 以上で求めた籠の最小サイズで最も小さいものの辺の長さが答え。
• エリアの広さは無限大なので、鼠の初期位置である±1000を超えるエリアでクロスすることもある点にチュウ意。

#include <string>
#include <vector>
#include <set>
#include <list>
#include <queue>
#include <algorithm>
#include <sstream>
#include <cmath>
#include <float.h> // DBL_MAX
using namespace std;

#define sz(a)   int((a).size())
#define pb      push_back
#define all(c)  (c).begin(),(c).end()
#define tr(c,i) for(typeof((c).begin()) i=(c).begin(); i!=(c).end(); i++)

double maxnum = DBL_MAX; // 平面が無限遠に伸びているので2000とか10000とかでは駄目です

class CatchTheMice {
public:
  double largestCage(vector<int> xp, vector<int> yp, vector<int> xv, vector<int> yv) {
    int n=xp.size(); // 1..50

    set<double> tx;
    tx.clear();

    // 全鼠総当たりで（高々1225通り）
    for (int i=0;i<n;i++) {
      for (int j=0;j<n;j++) {
        if (i < j)  {
          // x座標上で追い越し／追い越される時刻を得て
          if (xv[i] != xv[j]) {
            double t = (double)(xp[i] - xp[j]) / (double)(xv[j] - xv[i]);
            if (t > 0.0) tx.insert(t); // >0ならsetに放り込む。
          }
          // y座標上で追い越し／追い越される時刻を得て
          if (yv[i] != yv[j]) {
            double t = (double)(yp[i] - yp[j]) / (double)(yv[j] - yv[i]);
            if (t > 0.0) tx.insert(t); // 同様。重複はsetが良きに計らってくれる
          }
        }
      }
    }

    // t=0 における全鼠の座標と、wx=(x最大-x最小), wy=(y最大-y最小) を求めておく
    double wx_, wy_, t_ = 0.0; // ここでアンダーバーは「１つ前の値」マーク
    {
      double xmin = maxnum, xmax = -maxnum, ymin = maxnum, ymax = -maxnum;
      for (int i=0;i<n;i++) {
        double x = (double)xp[i];
        double y = (double)yp[i];
        if (x < xmin) xmin = x;
        if (x > xmax) xmax = x;
        if (y < ymin) ymin = y;
        if (y > ymax) ymax = y;
      }
      wx_ = xmax - xmin;
      wy_ = ymax - ymin;
    }
    double mmw = max(wx_,wy_); // 籠の大きさ

    // setに放り込んでおいた時刻をイテレータで順に取り出して
    // それぞれの時刻における全鼠の座標を算出し、
    // wx=(x最大-x最小), wy=(y最大-y最小) を求める。
    tr(tx,it) {
      double t = *it;
      double xmin = maxnum, xmax = -maxnum, ymin = maxnum, ymax = -maxnum;
      for (int i=0;i<n;i++) {
        double x = t*xv[i] + xp[i];
        double y = t*yv[i] + yp[i];
        if (x < xmin) xmin = x;
        if (x > xmax) xmax = x;
        if (y < ymin) ymin = y;
        if (y > ymax) ymax = y;
      }
      double wx = xmax - xmin;
      double wy = ymax - ymin;

      if (((wx_ < wy_ && wx > wy) || (wx_ > wy_ && wx < wy))) {
        // wx,wyの最大をとる座標軸が入れ替わる場合
        double dx = wx - wx_, dy = wy - wy_;
        double w = (wx_ * dy - wy_ * dx) / (dy - dx); // wはこの時刻における籠の大きさの最小値
        // printf("crossing between t=%g and t=%g... at %g\n", t_, t, (wx_ - wy_) / (dy - dx) );
        if (w < mmw) mmw = w;
      } else {
        // 入れ替わらない場合
        double w = max(wx,wy);
        if (w < mmw) mmw = w;
      }
      wx_ = wx;
      wy_ = wy;
      t_ = t;
    }

    return mmw;
  }
};

日本人参加者のランキングとか

18:11 |

https://www.otinn.com/groups/view_group.php?gid=1376

SRM425 Div1 Medium: PiecesMover

過去問, 練習 | 18:12 |

夕方の珈琲館で解いてみた。

1. ５つの駒を寄せた時に出来るパターンは571通り。駒の数が４つ以下ならもっと少ない。
   • 全パターン生成は 25C5 通りの組合せの中で５駒が繋がっているものを抽出。
   • ５駒が繋がっているかどうかを調べるのがこの問題で一番面倒な箇所かも
2. その全パターンに対し、5個の駒を寄せて移動数合計を調べ、合計最小移動数を求める
   • パーキングロット問題（最適ペアマッチング？）みたいだけど、最大5対5なので全ての組合せを調べても5!=120通りなので全部やる
   • 駒の初期位置が偏っている場合には盤のサイズを5x5より小さくできるが、特にやる意味はなさそう。

結論：冷静に考えればこれは余裕の問題。

#include <string>
#include <vector>
using namespace std;

#define sz(a)  int((a).size())
#define pb  push_back
#define all(c)  (c).begin(),(c).end()
#define tr(c,i)  for(typeof((c).begin()) i=(c).begin(); i!=(c).end(); i++)

class PiecesMover {

  // 駒の位置が立ったintを pair<int,int> のベクタに変換して返す
  vector<pair<int,int> > pattern(int x)
  {
    vector<pair<int,int> > ms(__builtin_popcount(x));
    int msi = 0;
    for (int i=0,m=1<<24; i<25; i++,m>>=1)
      if (x & m) ms[msi++] = make_pair(i/5,i%5);
    return ms;
  }

  // 駒がすべて繋がっているか調べる
  bool is_possible_pattern(const vector<pair<int,int> > &ms)
  {
    int n = sz(ms);
    vector<bool> ok(n,false), // 駒が#0から（直接もしくは間接的に）導通しているか
                    ck(n,false); // 調査済みか
    ok[0] = true;
    int okc = 1;

    bool om[7][7]; // 導通マップ
    for (int i=1;i<=5;i++) for (int j=1;j<=5;j++) om[i][j] = 0;

    while (1) {
      int cx = -1; // 未調査の駒を１つ選ぶ。（最初は 0 が選ばれる）
      for (int i=0;i<n;i++) if (ok[i] && !ck[i]) { cx=i; break; }
      if (cx == -1) break; // 未調査の駒がなくなればループ終了

      // 調査対象の駒の上下左右のセルを、導通マップ上でtrueにする。
      // 7x7にしてるのはここの便宜のため
      int x = 1+ms[cx].first, y = 1+ms[cx].second;
      om[x-1][y] = om[x+1][y] = om[x][y-1] = om[x][y+1] = true;

      // 未導通の駒iを探し、新たに導通していればok[i]をtrueにする
      for (int i=1;i<n;i++) {
        if (!ok[i]) {
          int x = 1+ms[i].first, y = 1+ms[i].second;
          if (om[x][y]) { ok[i]=true; okc++; }
        }
      }

      ck[cx] = true; // 調査済
    }

    // 全駒が導通していればtrue、さもなければfalseを返す
    return (okc == n);
  }

  // 2点間の距離
  int distance(pair<int,int> p1, pair<int,int> p2)
  {
    return abs(p1.first - p2.first) + abs(p1.second - p2.second);
  }
public:
  int getMinimumMoves(vector<string> board) {
    vector<pair<int,int> > pieces; // 駒の位置
    for (int r=0; r<5; r++)
      for (int c=0; c<5; c++)
        if (board[r][c]=='*') pieces.pb(make_pair(r,c));

    // すでに全駒導通していれば 0 を返す
    if (is_possible_pattern(pieces)) return 0;

    int N = sz(pieces), Nx = 1; // N=駒の数, Nx=N!
    for (int i=2; i<=N; i++) Nx*=i; // N!

    // 全ての導通パターンについて調べる
    int minimum_distance = INT_MAX;
    for (int i=(1<<25)-1; i>=0; i--) {
      if (__builtin_popcount(i) != N) continue;
      // ビットがN個立っているパターンのみ残る

      vector<pair<int,int> > pat = pattern(i);
      if (!is_possible_pattern(pat)) continue;
      // 全駒が導通しているパターンのみ残る

      vector<int> v(N); for(int i=0; i<N; i++) v[i] = i; // int v[5] = { 0,1,2,3,4 }
      for (int i=0; i<Nx; i++) { // N対Nの全組合せについて、合計移動距離を求め最小値と比較
        int total_distance = 0;
        for (int j=0;j<N;j++) total_distance += distance(pieces[j], pat[v[j]]);
        if (total_distance < minimum_distance) minimum_distance = total_distance;
        next_permutation(all(v));
      }
    }
    return minimum_distance;
  }
};

最悪のケースでも565msec前後で解けているようだ。

SRM425

11.12+.2008

TopCoder参加10回目。shinhさんと同じ部屋。

DIV	level	問題名	競技中	後で	System Test	備考
1	250	CrazyBot	◎			97.53%
1	500	PiecesMover	途中	o	passed	11/14 https://topcoder-g-hatena-ne-jp.jag-icpc.org/n4_t/20081114/p1
1	1000	(RoadsOfKingdom)	-

250点問題: CrazyBot

→OK。124.79点

最初 set<pair<int,int> > を使って書いたらぜんぜん帰ってこなかったのでvector<pair<int,int> > に変更。それでも遅いので vector<int> で書き直す。ローカルで5.8秒かかるのでシステムテスト通るか心配だったけど大丈夫だった。

・・・しかし、配列を再帰で渡さずにやる方法がある。そうすると0.1秒ぐらいで終わる。

速くならないかあれこれ考えるために時間を無駄にしたのが残念。

500点問題: PiecesMover

→時間切れ

あとでちゃんと解いてみる。

ハチロクTopCoder部チャットでnitoyonさんchokudaiさんtomerunさんらと雑談。isocchiさんがみんなのグラフを１つにしたのを作ってくれている。nishioさんおはようございます。

レーティング微減：1360 → 1342

そろそろ下げ止まりか。

今回の重要な教訓

うちのMacBook Proで6秒以内で終わるなら（タイムリミット２秒を恐れずに）submitしてしまおう。

（タイム縮められないかと思って無い知恵を絞って15分は無駄にしたので）

SRM424

参加9回目。

DIV	level	問題名	競技中	後で	System Test	備考
1	250	ProductOfDigits	◎			85.56%
1	600	StrengthOrIntellect	撃沈
1	900	(ProductOfPrices)	-

250点問題: ProductOfDigits

→OK。178.06点

250点問題は2,3,5,7で素因数分解。レーティング的にもID的にもご近所のTopCoder部のnで始まる他の皆さんも同じ発想だったようだ。しかしこれは9から順に割っていけば済む。なんというProjectEuler脳。

600点問題: StrengthOrIntellect

→×

残り１分でsubmitしたけど題意を読み違えててそもそもアウト...Orって書いてあるじゃん。Orって。

テストケース３番通らないけど問題おかしいんじゃない？と問題を疑ったら十中八九、いや百発百中で自分が間違っている。

しかしOrに直したやつでchokudaiさん作の撃墜ケースを通すと何分待っても帰ってこない。

nitoyonさんのとこ読んだら色々殆ど同じ感じ。

あと、自分のコードは撃墜できないというルールを知った。

900点問題

開いてない

レーティングまた落ちて 1417 → 1358。

ランキングに一喜一憂せず経験値を上げて挽回したい。2K狙いたいし。

SRM423 Div1 Easy: TheTower

過去問, 練習 | 18:12 |

撃墜された300点問題を解き直してみる。

競技中にsubmitしたコードではx(あるいはy)座標の平均値であたりを付けていたので撃墜されて当然・・・

とりあえず

　x: [ min(x) .. max(x) ]

　y: [ min(y) .. max(y) ]

の範囲にあるのは間違いないので、２重ループで総当たりしてみれば簡単なケースについては問題なく求められる。

#include <vector>
#include <algorithm>
using namespace std;

#define all(x)  (x).begin(),(x).end()

class TheTower {
public:
  vector<int> count(vector<int> x, vector<int> y) {
    int n = x.size();
    int xmin = *min_element(all(x)), xmax = *max_element(all(x)),
        ymin = *min_element(all(y)), ymax = *max_element(all(y));
    vector<int> m(n,INT_MAX); m[0] = 0;
    for (int x_=xmin; x_<=xmax; x_++) {
      for (int y_=ymin; y_<=ymax; y_++) {
        vector<int> d(n);
        for (int i=0;i<n;i++) d[i] = abs(x_ - x[i]) + abs(y_ - y[i]);
        sort(all(d));
        int a = d[0];
        for (int i=1;i<n;i++) {
          a += d[i];
          if (a < m[i]) m[i] = a;
        }
      }
    }
    return m;
  }
};

しかし x, y の値域はそれぞれ[1,1000000]なので、xmax - xmin と ymax - ymin が大きい場合にTLE。

ここで

　f(x,y) = Σ|x - xi| + Σ|y - yi|

が最小値をとるのは

　g(x) = Σ|x - xi|

　h(y) + Σ|y - yi|

がそれぞれ最小になる範囲である。それぞれが最小値をとるのは１点もしくは２点間の区間なので、その中に少なくとも１つの点(xj, yj)が含まれる。

従って、x,y座標とも、checkerのある座標のみ（各最大50）を調べればよく、

#include <vector>
#include <algorithm>
using namespace std;

#define tr(c,i)  for(typeof((c).begin()) i=(c).begin(); i!=(c).end(); i++)
#define all(x)  (x).begin(),(x).end()

class TheTower {
public:
  vector<int> count(vector<int> x, vector<int> y) {
    int n = x.size();
    vector<int> xs(all(x)); sort(all(xs));
    vector<int> ys(all(y)); sort(all(ys));
    vector<int> m(n,INT_MAX); m[0] = 0;
    tr(xs,x_) {
      tr(ys,y_) {
        vector<int> d(n);
        for (int i=0;i<n;i++) d[i] = abs(*x_ - x[i]) + abs(*y_ - y[i]);
        sort(all(d));
        int a = d[0];
        for (int i=1;i<n;i++) {
          a += d[i];
          if (a < m[i]) m[i] = a;
        }
      }
    }
    return m;
  }
};

O(n^3)だけどn≦50なのですぐに終わる。

追記

nitoyonさんの解説とは考える順番が逆かな。